

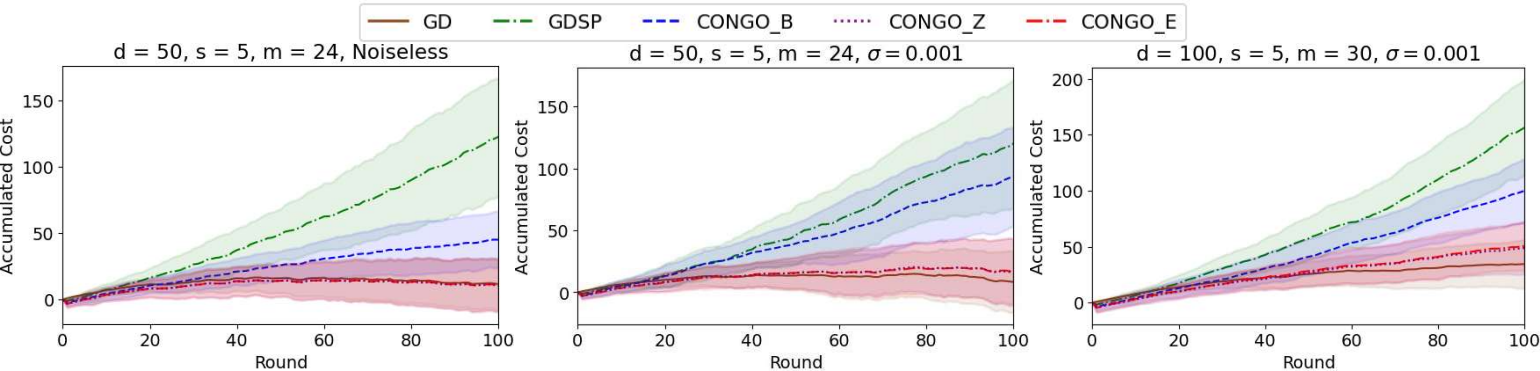
We address the challenge of zeroth-order online convex optimization where the objective function’s gradient exhibits sparsity. Our aim is to leverage this sparsity to obtain estimates of the objective function’s gradient when only a limited number of function samples are available. We tackle this problem by introducing the Compressive Online Gradient Optimization framework which allows compressive sensing methods previously applied to stochastic optimization to achieve regret bounds with an optimal dependence on the time horizon. Moreover, the number of samples required is only logarithmic in the full problem dimension. We use simulations and a microservice autoscaling problem to demonstrate CONGO’s superiority over gradient descent approaches that do not account for sparsity